Machine learning faces the problem of inductive risk, since it depends on human considerations, but also because it makes inferences based on empirical data. This is the case for both stages of scientific modelling. In the first phase, model construction runs the risk of the necessary process of feature extraction. And in the second stage, thresholds set by scientists influence the validation of the model. However, induction is the core of machine learning and epistemic values cannot help to overcome this problem. Therefore non-epistemic values are necessary to outbalance the outcomes of these algorithms. In the best case, they help us to reconsider our background assumptions and thus our values.

In the following sections, after giving some brief background information on machine learning, I will address three issues. First, the general problem of induction and the question what we actually learn through machine learning. Second, I will examine the construction of machine learning models with a focus on feature extraction. And lastly, the process of the validation of these models will be discussed.

Machine Learning

Machine learning is, broadly speaking, known as the task of analyzing large amounts of data and creating artificial “knowledge” based on patterns found in the data. There are mainly two distinct approaches, namely supervised and unsupervised learning. Supervised learning is the task of approximating a target function f that maps the input data X to the predicted output data Y through inference. In its simplest form looking like: Y = f(x)

IDFeature 1Feature 2…Output Class Y
x1[-199.35, 123.45, 30.17][-259.49, 143.36, -46.03]cat
x2[-41.26, 169.62, 37.72][11.58, 188.05, -45.03]cat
x3[50.35, 182.59, 154.33][44.34, 175.44, 61.90]dog
…

In order to find the target function f the algorithm is trained with available data, called training set which is labelled accordingly. Through labelling, which gives meaning to the data by the scientist (see Table), the computer algorithm is then able to solve classification or regression problems. So for example, the model can classify pictures into “cat” and “non-cat”, but also make predictions where future inputs result in an output based on previous training data, such as the trend in housing prices. In unsupervised learning, on the contrary, the output data is not available, thus the labeling of data does not occur. This means that the algorithm is more “autonomous” when it comes to finding patterns in the data. For the remainder of this paper, however, the emphasis will be placed only on supervised learning.

Dangers and Benefits of Inductive Risk

Machine learning relies on empirical data to make an inductive inference from observations to a hypothesis. Therefore, it faces the problem of inductive risk. First of all, however, the question arises what the predictions of machine learning algorithms actually tell us? With the Scottish philosopher David Hume in mind, who popularized the problem of induction, merely that the future will resemble the past.

At first glance, this seems to pose a threat to what Lakatos calls a degenerative problem-shift that does not create any novel research problems (Lakatos, 1968, p.164). In a sense, because we tend to see the world the way we want to see it based on past experience. For example, when we think of the problem of filter bubbles we are less and less confronted with opposing world views. Moreover, the idea that the future resembles the past, gives us examples of how Amazon has developed an algorithm for recruiting new staff which only hired males (Dastin, 2018). Even though the model might be correct from an epistemological point of view, such as accuracy or simplicity, it questions non-epistemic values, such as fairness. Several other examples of biases in machine learning algorithms raise the question whether the models help us to predict the future adequately, and thus confirm with our hypothesis, or whether they rather describe current social circumstances, i.e. non-epistemic values? Which leads us back to the initial question:

What do we actually learn through machine learning?

The answer might be twofold. On the one hand, machine learning gives us the possibility to gain new insights, thus also creating new research problems, as the recent case of the coronavirus prediction shows (Niiler, 2020). But on the other hand, it may also produce questionable predictions, such as Amazon’s recruiting tool. In the best case, these questionable predictions, give us the chance to reevaluate our hypothesis and background assumptions and thus to overcome certain biases. In the end this would help us to achieve a higher degree of ‘objectivity’ (Longino, 1998, p.181). In this case, ‘objectivity’ is meant as some sort of overarching non-epistemic values, such as fairness and equality. Even though this might be impossible to achieve, ‘everyone’ is nevertheless aware that gender inequality should not be tolerated.

The process of being aware of ones own assumptions and values, however, is very difficult, since they are most likely apparent in the entire culture one is living in. This refers to Longino who claims that knowledge is “social knowledge” (Longino, 1998, p.180). Okruhlik (1998) argues similarly, namely that social influences do not only affect the context of justification, but also the context of discovery, in this case model construction. Another problem arises with regard to Popper’s falsification approach. We cannot be sure what we have falsified: the hypothesis, the auxiliary assumptions, or even both? Consequently, under these considerations, it appears that the risks of drawing conclusions from machine learning outweigh the benefits.

In the case of Amazon the false hypothesis and background assumptions were found rather quickly. But there could be more subtle biases around us which we are not yet aware. This again shows the twofold consequences in terms of inductive risk: The danger of scientists implementing these biases into the algorithms and the benefit of amplifying these biases, and thus making them visible to us.

Nevertheless, Morrison and Morgan (1999) argue that models are used to learn and understand the target system. In how far this is the case with machine learning models might be debatable considering the problem one is trying to solve. However, since supervised learning relies on a human, i.e. a supervisor so to speak, who labels the data, it is prone to inductive risk. In the following sections I will show that, on the one hand, induction is necessary for machine learning to function. This is especially the case in the process of model construction. But, on the other hand, it also poses dangers when scientists only consider epistemic values while choosing a model, which is considered in the stage of model validation. Consequently, non-epistemic values are necessary to outbalance inductive risk.

Model Construction

Models are considered as “autonomous agents” (Morrison & Morgan, 1999, p.10). In the case of machine learning algorithms, they are autonomous in two ways. First, they are “partially independent of both theories and the world” (Morrison & Morgan, 1999, p.10). This means they can be used as instruments in order to represent the desired target system or natural phenomena. Second, the algorithms are autonomous in the sense of improving through additional data and thus without human intervention. But as Morrison and Morgan also state, models cannot be derived from theory or data alone. Rather, models require some “additional ‘outside’ elements” (Morrison & Morgan, 1999, p.11). In the case of supervised learning the labelling of the data can be considered as such an element, but also the process of feature extraction. The latter marks a very important role in the construction of machine learning models. Although some algorithms, such as the Convolutional Neural Network, are capable of automatic feature extraction, this task is considered as human activity in the following, since other algorithms depend on it.

Feature extraction is the practice of defining which features, i.e. information, contained in a collected data set are relevant for the representation of a given phenomena. In other words, which data is relevant in regard to ones hypothesis and auxiliary assumptions. Since the world around us is a constant stream of empirical data, especially in the technological sphere, data collection should not be a major hurdle. Empirical data, however, are “algorithmically random strings of digits” (McAllister, 2003, p.639). This means that scientists have to make sense of the random data that consists of a lot of noise, that is unnecessary information. Since this unnecessary information is discarded, feature extraction is a critical task. Besides, computational considerations have to be taken into account as well, to assure the algorithms can process the extracted data more precisely. A related problem with the selection of features is the so-called curse of dimensionality. This says, the more characteristics are considered in a feature vector, the more examples are needed to differentiate each features from each other (Bishop, 2006, p.35). In other words, the fewer features, the better, since less data is needed. So, the main challenge is to find features that represent the phenomena correctly and that can be “easily” computed.

As there are no specific rules to feature extraction, since it also depends heavily on the problem one is trying to solve, it can be compared to some craftsmanship, as Morrison and Morgan (1999) do with model construction. As we can see, machine learning is very much dependent on human intelligence. Especially on human induction, otherwise there would be no training data and thus no model.

While processing the data, i.e. building and manipulating the model, scientists gain new insights. Throughout several iterations of model creation and model validation, scientists might interpret certain features differently. This results in new correlations the scientist can draw that increase the “understanding of a complex real-world system” (Godfrey-Smith, 2006, p.726).

Often, however, we do not learn about the cause of an effect. This is because correlation does not imply causation. In machine learning it is the output through which scientists learn, although without necessarily understanding the causal chain. For feature extraction this means, that certain features could be more or less important than considered. This becomes all the more apparent the more complex and autonomous the algorithms become. As a result, it becomes increasingly difficult to fully understand how the algorithms function. This goes against the account of Knuttila and Merz (2009) who claim that models themselves help us to learn through the objectual approach. But as Morrison and Morgan mention, models do not “require extensive knowledge of every aspect of the system.” (Morrison & Morgan, 1999, p.31). Nevertheless, this unawareness brings us back to initial question: what do we actually learn through machine learning models? Furthermore, the incomprehensible, or incommensurable, outcome has ethical consequences as new effects result in another chain of causes and effects. Thus, the typical scientific question “Why does this phenomenon occur” becomes harder to answer.

For these two reasons, the human induction through feature extraction and the increasing incomprehensibilty of the outcome, non-epistemic values are necessary for model construction. This aligns whit Okruhlik’s (1998) argument that the context of discovery, which can be viewed as model construction, is influenced by sociological factors.

Model Validation

The second stage is the model validation, in this case also called the testing phase. To test the model, the scientists again present labelled data to the model, which is different to the training data, and compare the predicted outcome with the true result. Since models always represent the phenomena and not the data, there seem to be epistemic values when it comes to the choice of models. This is because in machine learning there are cases where underfitting or overfitting in respect to the data occur.

Problems of underfitting and overfittig in machine learning (Shapire, n.d.).

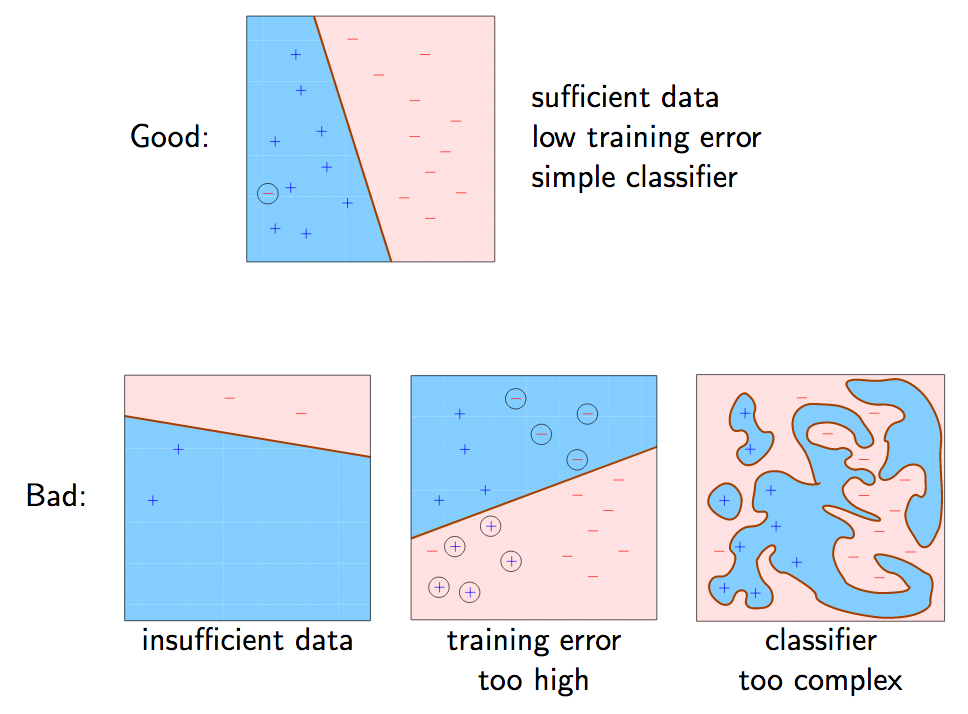
This is similar to Douglas’ (2000) account of epistemic significance. In the case of underfitting, the algorithm has either too little data to find an appropriate mapping function, or the testing phase resulted in an error rate which exceeded a certain threshold. In the case of overfitting, the algorithm did not make general inferences, but rather learned one-to-one. If overfitting occurs, then the model does not represent the phenomena anymore, but rather the data. According to Morrison and Morgan, however, this should not happen because the independence of the model is not guaranteed anymore (Morrison & Morgan, 1999, p.17). Therefore, overfitted algorithms are not of real world use.

This lets the case for the epistemic significance, which basically balances out false positives and false negatives. Although there are different accuracy and error optimization functions available in model validation, they still depend heavily on the threshold the scientists set. That is, in the case of a binary distinction, a value which labels the outcome as either true or false. So for example, to classify an email as spam or not spam, the scientists have to extract each word and assign a sentiment score, or weight, to it. If the sum of all words, i.e. weights, reach a certain threshold, the algorithm classifies the email accordingly. As we can see, the threshold in this simple example is crucial, but more important, defined by a human who infers certain values into the system. Therefore, when defining these thresholds, we have to consider non-epistemic values according to the problem.

Confusion matrix of two Neural Networks. The number below represents the structure of the Neural Network, so 450 neurons in the first layer.

Another problem is the choice of model. Since there are unlimited possibilities to model machine learning algorithms, it seems difficult to choose the one that adequately represents the target system. In general, certain types of models are better suited for certain tasks. Nevertheless, it might happen that two different models, for example a Neural Network and a Support Vector Machine both are equally suitable for the given task to date. At this point it seems that the scientist is free to choose which one to use. By doing so, however, he or she faces the risk of not being able to foresee certain consequences. It might happen, that with increasing training data, the Support Vector Machine will outperform the Neural Network for this specific hypothesis. This briefly refers to the No Free Lunch Theorem, which more or less says that there is not one model that is suitable for all possible situations. Besides, the choice of model also faces the problem of underdetermination, since we should not choose a model based on empirical data. Yet, empirical data is the core of machine learning.

However, even if scientists manage to set adequat thresholds and are able to choose the ‘correct’ model, the main problem of induction in the stage of model construction still remains. This means, even though the predictions might be accurate, the scientist cannot be certain that his or her underlying hypothesis and/or background assumptions are true. As Okruhlik (1998) puts it, the context of discovery cannot and the context of justification cannot be separated.

Conclusion

As we can see, the problem of inductive risk exists in both stages. In model construction it is the case due to the task of feature extraction. In this process, scientists give meaning to random data sets, and since data has to be modeled differently in different problem settings, there are no general rules to it – what makes it comparable to arts. Therefore, non-epistemic values are needed, as several biased algorithms show. In the case of model validation, thresholds play a crucial role, which again are defined by the scientists. Although there are epistemic values, such as accuracy, the outcome is still dependent on these thresholds. So, also for model validation non-epistemic values have to be taken into account.

Since machine learning algorithms have real world implications they can have positive but also negative consequences, as the two presented cases show, namely the Amazon recruiting tool and the prediction of the coronavirus. Nevertheless, the question remains what we actually learn from these predictions? This is because the underlying assumption of induction is that the future resembles the past. This inference faces either the challenge of us being stuck in societal bias and thus a degenerating problem-shift. Or it helps us to reevaluate our background assumptions, thus biases, which would lead to a higher degree of ‘objectivity’ and also to a progressive problem shift. In this case ‘objectivity’ is considered as some sort of overarching non-epistemic values, such as equality and fairness. The outcome, however, is probably highly dependent on who, i.e. the diversity of social groups, has a say in the process of model construction and validation. But this is a different discussion.

References